Matriks
Matriks
• Pengertian Matriks
Matrik adalah susunan bilangan real (kompleks) berbentuk empat persegi panjang yang dibatasi oleh tanda kurung, ditulis dengan :
Istilah-Istilah Matriks
- Lambang-lambang matriks menggunakan huruf kapital (A,B,C,D,...,Z)
- Elemen matriks menggunakan lambang huruf kecil (a,b,c,d,...,z)
- Bagian mendatar/horizontal disebut baris
- Bagian tegak/vertikal disebut kolom
- Indeks "i" menyatakan baris dan indeks "j" menyatakan kolom
- Jumlah baris = m dan jumlah kolom = n
- Matriks dengan jumlah baris = m dan jumlah kolom = n disebut dengan ukuran (m x n) atau berordo (m x n)
- Elemen matrik dapat berupa bilangan bulat, desimal, riil atau kompleks.
Contoh
Beberapa istilah yang perlu diketahui ;
• Elemen matrik A dapat berupa bilangan bulat, desimal, riil atau bilangan kompleks
• Jumlah baris a=4, jumlah kolom a=5, A berukuran (4x5)
• a32 : elemen baris ke-3 kolom-2 adalah 0.001
• Elemen-elemen diagonal matrik A : 1, π, √3, 1
Matrik jaringannya adalah sebagai berikut
JENIS - JENIS MATRIK
Matrik Bujur Sangkar
A dikatakan matrik bujur sangkar jika jumlah baris dan jumlah kolom A sama. Matrik A dikatakan berordo n
Elemen-elemen diagonal utama A adalah a11, a22, a33, a44 ….
Contoh
MA berordo 4, elemen-elemen diagonal utama A adalah 0, 0, 0, 0
Matrik Segitiga Atas
A dikatakan matrik segitiga atas, jika A adalah matrik bujur sangkar dimana semua elemen dibawah diagonal utama 0
Elemen-elemen diagonal utama : 3, 9, -7, 2, 8
Elemen-elemen dibawah diagonal utama 0, maka A matrik segitiga atas
Matrik Segitiga Bawah
A dikatakan matrik segitiga atas, jika A adalah matrik bujur sangkar dimana semua elemen diatas diagonal utama 0
Elemen-elemen diagonal utama : 1, 4, 7, 2, 8
Elemen-elemen diatas diagonal utama 0, maka A matrik segitiga bawah
Matrik Diagonal = D
A dikatakan matrik diagonal, jika A adalah matrik bujur sangkar dimana semua elemen selain diagonal utama 0, dan elemen diagonal utama tak nol. Matrik demikian diberi lambang D.
Matrik Identitas = I
A dikatakan matrik identitas, jika A adalah matrik bujur sangkar dimana semua elemen selain diagonal utama 0, dan elemen diagonal utama 1. Matrik identitas diberi lambang I.
Transpose Matrik= AT
Transpose matrik A ditulis AT adalah sebuah matrik yang diperoleh dari A dimana baris AT adalah kolam A, dan kolom AT adalah baris A. Bila A berukuran (mxn), AT berukuran (nxm)
CONTOH
Matrik Simetris, A=AT
A dikatakan matrik simetris, bilamana A adalah matrik bujur sangkar dimana, AT=A
CONTOH
Matriks Baris
Matriks Baris adalah matriks yang terdiri dari satu baris
Contoh : A = ( 1 3 4 9)
Matriks Kolom
Matriks Kolom adalah matriks yang terdiri dari satu kolom
Contoh
Matriks Nol
Matriks Nol adalah Suatu matriks yang setiap unsurnya 0 berordo ,ditulis dengan huruf O.
Contoh
Matriks Skalar
Matriks Skalar adalah matriks diagonal yang unsur-unsur pada diagonal utama semuanya sama.
Matriks Mendatar
Matriks Mendatar adalah matriks yang banyaknya baris kurang dari banyaknya kolom .
Matriks Tegak
Matriks Tegak adalah suatu matriks yang banyaknya baris lebih dari banyaknya kolom.
Matriks Skew Simetris
Matriks Skew Simetris (Anti Simetri), yaitu suatu matriks persegi yang apabila ditransposkan akan sama dengan negatif dari matriks semula. Misalkan A adalah matriks persegi. Matriks A dikatakan skew simetris jika dan hanya jika AT=−A. Syarat lainnya yaitu semua elemen yang berada di diagonal utama bernilai nol.
OPERASI ARITMATIK MATRIK
(1) Matrik, A=[aij] dan B=[bij] dikatakan sama ditulis A=B jika hanya jika
• A dan B berukuran sama
• Setiap elemen yang seletak nilainya sama, aij = aij ;
Contoh :
A dan B berukuran sama (2x3), tetapi AB, karena terdapat elemen seletak nilainya tidak sama
(2) Perkalian dng skalar, kA
Perkalian matrik, A=[aij] dengan skalar tak nol k ditulis kA, didefinisikan bahwa setiap elemen A dikalikan dengan konstanta tak nol k, yakni :
kA=k[aij]= [kaij]
Contoh :
(3) Penjumlahan, A+B
• Bilamana, A+B=C, maka elemen matrik C diberikan,
cij = aij + bij
(elemen yang seletak dijumlahkan)
Contoh :
Diberikan :
(4) Perkalian Matrik, AB=C
(1) Matrik, A=[aij](m=n) dan B=[bij](pxq) dikatakan dapat dikalikan ditulis AB bilamana jumlah kolom A dan jumlah baris B sama [n=p].
(2) Bilamana, AB=C, maka matrik C=[cij](mxq) dimana elemen cij diberikan oleh :
Contoh :
Diberikan :
Sifat Penjumlahan Matrik
Misalkan terdapat matriks A,B,C dan matriks nol O sedemikian rupa sehingga berlaku :
A+B=B+A
A+(B+C)=(A+B)+C
A+O=O+A=A
A+(−A)=−A+A=O
Sifat Perkalian Matrik
Misalkan terdapat matriks A,B,C, matriks nol O, matriks identitas I dan m,n sembarang bilangan bulat yang sedemikian rupa sehingga berlaku :

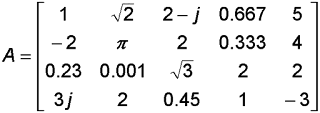






















Komentar
Posting Komentar